Amortized Bayesian inference on generative dynamical networkmodels of epilepsy using deep neural density estimators- 논문 리뷰 3

3. Results

3.1. The SBI-VEP against source-level epileptic patterns

제공된 그림에는 베이지안 추론을 이용한 간질성 뇌 활동에 대한 공간적 분포 맵의 추정과 관련된 네 가지 주요 부분이 나타나 있습니다.

A)Observed source activity (관찰된 소스 활동): 뇌의 다양한 영역에서 관찰된 신경 활동의 시간에 따른 변화를 보여줍니다. 여기서 각 선은 뇌의 특정 영역에서의 실제 전기적 활동을 나타내며, 색상은 간질성 영역(EZ: epileptogenic zone)을 나타내는 빨간색과 전파 영역(PZ: propagation zone)을 나타내는 노란색으로 구분되어 있습니다.

B) Predicted source activity (예측된 소스 활동): 시뮬레이션 기반 추론 (SBI)과 신경 밀도 추정기를 통해 훈련된 모델이 생성한 신경 활동의 예측치를 보여줍니다. 이는 A의 관찰된 데이터와 비교될 수 있으며, 예측 모델이 얼마나 잘 관찰 데이터를 재현하는지를 보여줍니다.

C) Posterior \( \eta_i \) for all brain regions (모든 뇌 영역에 대한 사후 분포 \( \eta_i \)): 모든 뇌 영역에 대한 매개변수 \( \eta_i \)의 사후 분포를 나타내며, 이는 각 뇌 영역의 간질 발생 가능성을 나타냅니다. 여기서 EZ, PZ, HZ (healthy zone, 건강한 영역)는 각각 다른 발작 기원 가능성을 가진 영역을 나타냅니다. 검은색 원은 관찰 데이터를 생성하기 위해 사용된 실제 값들을 나타냅니다.

D) Diagnostics (진단도구): 사후 분포의 z-점수와 축소 값(shrinkage)의 분포를 통해 모델이 데이터를 얼마나 잘 학습했는지 진단합니다. 이상적인 Bayesian 역전이 바닥 오른쪽으로 향하는 경향을 가질 때 나타나며, 이는 모델이 데이터에서 정보를 잘 추출했음을 나타냅니다. z-점수가 낮고 축소 값이 높으면 이상적인 적합을 의미하며, 반대의 경우에는 모델이 데이터를 잘 반영하지 못했음을 나타낼 수 있습니다. 이 그래프는 모델의 성능을 진단하고 어떤 매개변수가 잘 식별되지 않았는지, 혹은 과적합이 있는지 등을 판단하는 데 사용됩니다.

3.2. The SBI-VEP against phase-plane dynamics

이 그림은 간질 관련 동적 뇌 모델의 페이즈 플레인(phase plane) 분석을 보여줍니다. 페이즈 플레인 분석은 뇌의 특정 영역들이 시간에 따라 어떻게 변화하는지를 2차원 공간에 표현한 것입니다. x축과 z축은 각각 뇌 영역의 두 가지 다른 동적 변수를 나타냅니다. 이러한 분석을 통해, 시스템의 동적 안정성과 발작의 발생 및 전파와 같은 동적 현상을 이해할 수 있습니다.

A) Healthy Zone (HZ)의 페이즈 플레인: 건강한 뇌 영역에서 관찰된(녹색 선) 및 예측된(검은 점선) 동적 궤적을 보여줍니다. HZ는 단일 안정된 고정점을 나타내며, 이는 해당 지역이 간질원성이 아니라는 것을 의미합니다. 여기서 뇌의 활동은 한 지점 주변에서 안정적으로 유지됩니다. 즉, 발작이 일어나지 않는 정상 상태를 보여주죠.

B) Propagation Zone (PZ) with Global Coupling K = 0: 전파 영역의 페이즈 플레인으로, 전역 커플링 매개변수 K가 0으로 설정된 경우를 나타냅니다. 여기서 발작의 전파는 복잡한 네트워크 효과를 통해 발생합니다. 
(전파 지역은 발작이 시작되지는 않지만, 다른 곳에서 시작된 발작이 여기로 퍼질 수 있는 곳입니다. K=0이라는 건 이 지역이 다른 영역들과 얼마나 강하게 연결되어 있는지를 나타내는 값이 0이라는 뜻이에요. 이 경우엔 발작이 퍼지기 어렵죠.)

C) Propagation Zone (PZ) with Global Coupling K = 1: K가 1일 때 PZ의 페이즈 플레인입니다. PZ의 평형이 분기점에 가까워서 발작이 이 지역으로 전파될 수 있습니다.
(여기서는 K 값이 1로, 이는 이 지역이 다른 영역들과 더 강하게 연결되어 있음을 의미해요. 그래서 발작이 이 지역으로 더 쉽게 퍼질 수 있죠.)

D) Epileptogenic Zone (EZ)의 페이즈 플레인: EZ에서 관찰된(빨간색 선) 및 예측된(갈색 점선) 동적 궤적을 보여줍니다. EZ는 불안정한 고정점을 나타내어 발작의 시작이 지역의 본질적인 속성임을 나타냅니다.
(이곳은 발작이 시작되는 곳입니다. 불안정한 지점 주변의 뇌 활동은 발작이 시작될 수 있는 상태를 나타냅니다.)

각 패널의 푸른색 선들은 등고선을 나타내며 시스템의 안정성과 불안정성을 나타냅니다. 채워진 및 빈 원은 각각 시스템의 안정된 및 불안정한 고정점을 나타냅니다. 이러한 고정점은 시스템의 다양한 동적 상태를 이해하는 데 중요한 정보를 제공합니다.

쉽게 말해, 이 그림들은 뇌의 각 부분이 발작을 어떻게 시작하고 전파하는지를 나타내는 시뮬레이션 결과를 보여주는 것이에요. 안정적인 지점(채워진 원)은 발작이 일어나지 않는 정상 상태, 불안정한 지점(빈 원)은 발작이 발생할 수 있는 상태를 의미합니다.

3.3. The SBI-VEP against SEEG data

이 그림은 간질에 관한 연구에서 사용된 SEEG (stereoelectroencephalography) 데이터의 Bayesian 분석을 보여줍니다.

A) 관찰된 SEEG 데이터 (Observed SEEG data): 이것은 실제로 환자의 뇌에서 관찰된 SEEG 신호의 여러 트레이스(선)를 보여줍니다. 이 데이터는 뇌의 전기적 활동을 시간에 따라 측정한 것입니다. 

B) 예측된 SEEG 데이터 (Predicted SEEG data): 여기에 표시된 것은 모델을 사용하여 생성된 예측된 SEEG 데이터입니다. 이 데이터는 A의 실제 관찰된 데이터를 바탕으로 만들어졌으며, 신호의 변화 패턴이 유사한 것을 볼 수 있습니다.

C) 모든 뇌 영역에 대한 사후 분포 (Posterior distribution for all brain regions): 이 바 그래프는 각 뇌 영역에 대한 매개변수 \( \eta_i \)의 사후 분포를 보여줍니다. EZ(간질원성 영역), PZ(전파 영역), HZ(건강한 영역)는 각각 다른 색으로 표시되어 있습니다. 검은색 원은 관찰된 데이터를 생성하기 위해 사용된 실제 값들을 나타냅니다. 즉, 높이는 발작이 일어날 확률을 나타내고, 검은 점은 실제 발작이 일어난 곳을 나타냅니다. 색깔은 발작이 일어난 부분을 나타내요: 빨강은 발작 지역(EZ), 노랑은 발작이 퍼질 수 있는 지역(PZ), 초록은 정상 지역(HZ)을 말합니다.

D) 진단도구 (Diagnostics): 이것은 사후 분포의 z-점수와 축소 값(shrinkage)의 분포를 통해 모델이 얼마나 잘 학습했는지 평가하는 도구입니다. z-점수가 낮고 축소 값이 높으면 모델이 데이터를 잘 적합시켰음을 의미합니다. 그래프에서 볼 수 있듯이, 대부분의 지점들이 이상적인 적합 범위 내에 위치해 있습니다. 즉, 여기서는 컴퓨터 모델이 얼마나 잘 예측했는지를 점수로 보여줍니다. 축소(shrinkage) 값이 낮을수록 (왼쪽으로 갈수록), 모델이 실제 데이터와 잘 맞지 않는 거예요. 반대로 오른쪽으로 갈수록 잘 맞는다는 뜻입니다.

이 그림 전체적으로 보면, 연구진은 SEEG 데이터를 사용하여 뇌의 각 영역에서 간질 발생 가능성을 평가하고 있으며, 예측 모델이 실제 데이터와 얼마나 잘 일치하는지를 보여주고 있습니다. 이를 통해 특정 뇌 영역이 발작을 일으킬 가능성이 있는지, 아니면 정상적인지를 판단할 수 있습니다.

3.4. Algorithmic benchmark on the SBI-VEP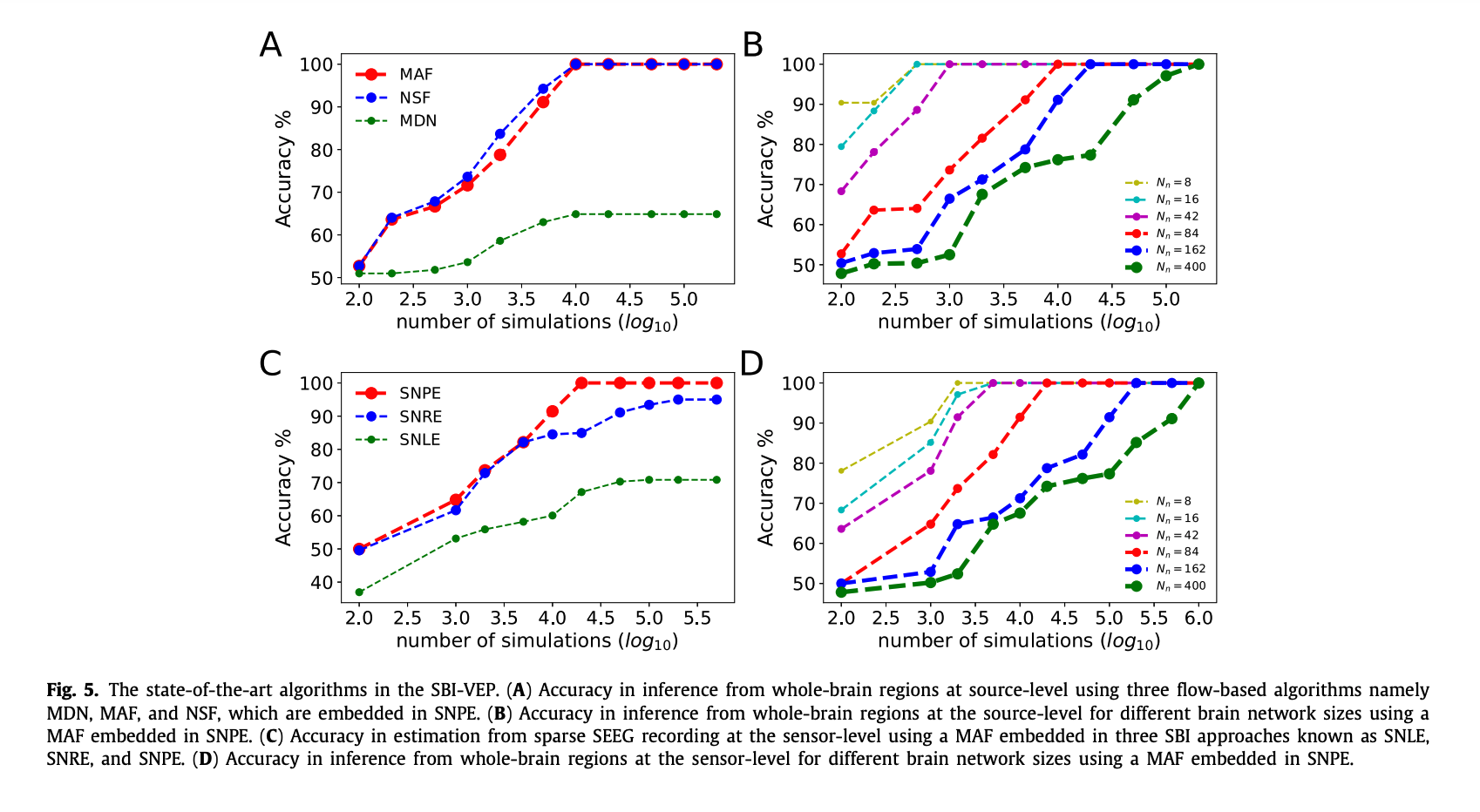

그림 5에서는 여러 가지 최첨단 알고리즘들의 성능을 비교하고 있는데요, 모두 시뮬레이션 기반 추론(Simulation-Based Inference, SBI)에 관련된 알고리즘들입니다. 이 그림들은 알고리즘들이 뇌 신호 데이터를 얼마나 정확하게 추론할 수 있는지 보여주고 있어요. x축은 시뮬레이션 횟수를 로그 스케일로 나타내고, y축은 추론 정확도를 퍼센트로 나타냅니다.

A) 다양한 flow-based 알고리즘들의 정확도: 여기서는 MAF (Masked Autoregressive Flow), NSF (Neural Spline Flows), 그리고 MDN (Mixture Density Networks) 세 가지 알고리즘의 정확도를 보여주고 있습니다. 이들은 모두 SNPE (Sequential Neural Posterior Estimation) 방법에 내장된 알고리즘들입니다. MAF가 가장 높은 정확도를 보여주고 있네요.

B) 뇌 네트워크 크기에 따른 정확도: 이 그래프는 뇌 네트워크의 크기 \( N_n \)가 작을수록(예: \( N_n = 8 \)) 높은 정확도를 달성한다는 것을 보여줍니다. 더 큰 네트워크(예: \( N_n = 400 \))에서는 더 많은 시뮬레이션 횟수가 필요하여 정확도가 낮아집니다.

C) SBI 접근 방식에 따른 정확도 그래프 (Accuracy graph): 이 부분은 세 가지 다른 시뮬레이션 기반 추론(Simulation-Based Inference, SBI) 기법의 정확도를 비교하고 있어요. SNPE가 가장 높은 정확도를 보여줍니다.

• SNPE (Sequential Neural Posterior Estimation): 빨간색 원표로 표시된 선은 SNPE 방법의 정확도를 나타냅니다. 이 방법은 시간이 지날수록 가장 높은 정확도를 보여줘요.
• SNRE (Sequential Neural Ratio Estimation): 파란색 점선은 SNRE 방법의 정확도를 나타냅니다. SNPE보다 조금 낮은 정확도를 보이는 것으로 나타나네요.
• SNLE (Sequential Neural Likelihood Estimation): 초록색 점선은 SNLE 방법의 정확도를 나타냅니다. 이 방법은 두 방법 중 가장 낮은 정확도를 보여줍니다.

D) 뇌 네트워크 크기에 따른 정확도 (Accuracy by brain network size): D 그래프에서는 실제로 뇌 네트워크의 크기 \( N_n \)가 작을수록 더 높은 정확도를 달성하는 것을 보여줍니다. 이는 더 작은 네트워크에서는 매개변수를 추정하는 데 필요한 정보가 더 적기 때문에 정확도가 높게 나타날 수 있음을 의미합니다. 반면에, 더 큰 네트워크에서는 더 많은 정보가 필요하고, 이를 처리하는 데 더 많은 시뮬레이션 횟수가 필요하므로 정확도가 낮아질 수 있습니다. 

전반적으로 이 그림들은 뇌의 전체적인 영역에서 더 정확한 추론을 하기 위해서는, 어떤 SBI 기법을 사용하는지, 뇌 네트워크의 크기가 얼마인지가 중요하다는 것을 보여주고 있습니다. SNPE 방법이 전체적으로 높은 정확도를 보이는 것으로 나타나고 있습니다.

3.5. The SBI-VEP against empirical SEEG recordings


4. Discussion